几何是初中数学最主要的内容,对大多数孩子来说也是比较难的内容。而我们想要战胜这一比较难的题型,我们就需要多多练题。
经典难题(一)
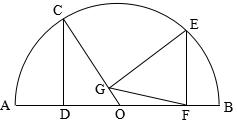
1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.
求证:CD=GF.(初二)
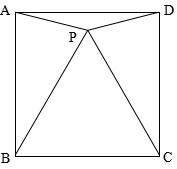
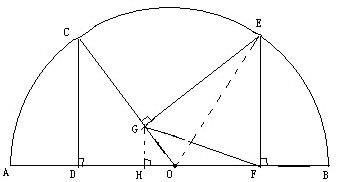
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15度
求证:△PBC是正三角形.(初二)
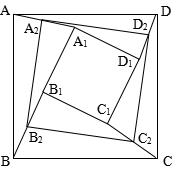
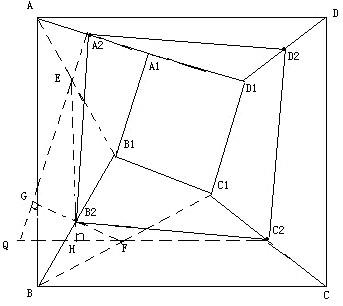
3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.
求证:四边形A2B2C2D2是正方形.(初二)
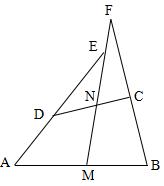
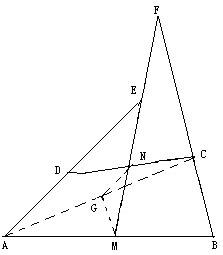
4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.
求证:∠DEN=∠F.
经典难题(二)
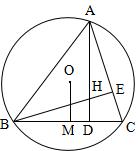
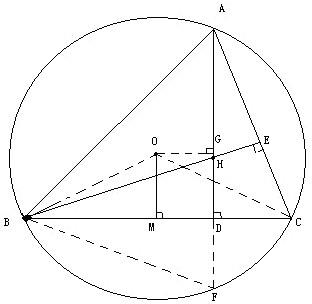
1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.
(1)求证:AH=2OM;
(2)若∠BAC=600,求证:AH=AO.(初二)
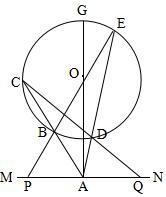
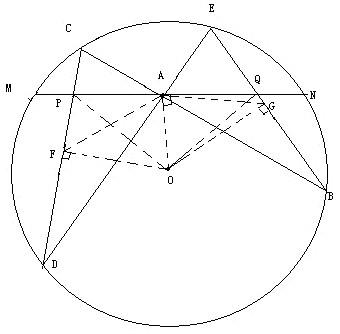
2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.
求证:AP=AQ.(初二)
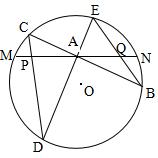
3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:
设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.
求证:AP=AQ.(初二)
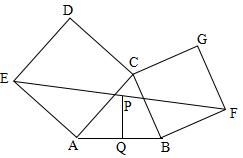
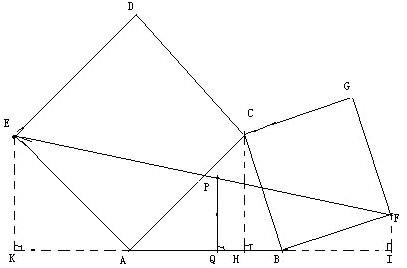
4、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点.
求证:点P到边AB的距离等于AB的一半.(初二)
经典难题(三)
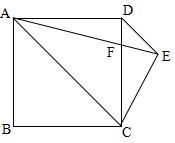
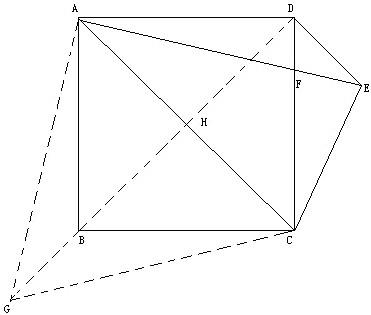
1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.
求证:CE=CF.(初二)
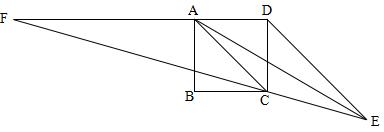
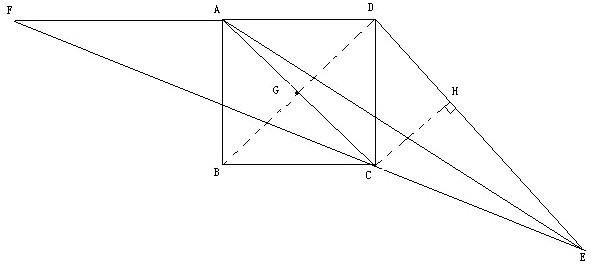
2、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC交DA延长线于F.
求证:AE=AF.(初二)
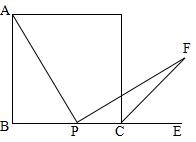
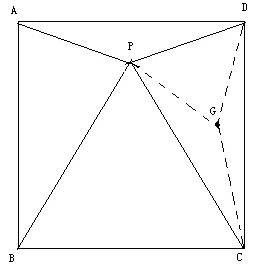
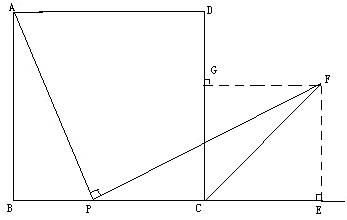
3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.
求证:PA=PF.(初二)
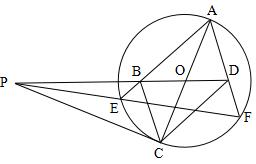
4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)
经典难题(四)
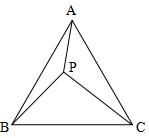
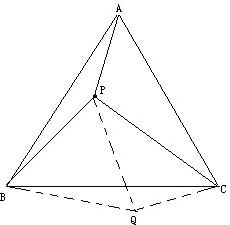
1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.
求:∠APB的度数.(初二)
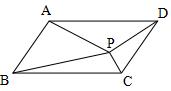
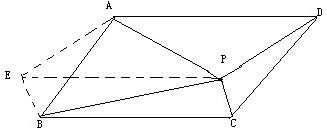
2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.
求证:∠PAB=∠PCB.(初二)
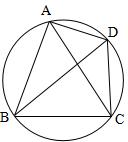
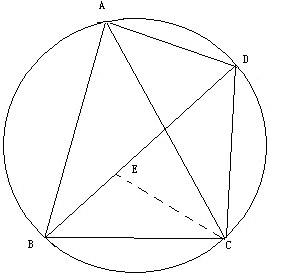
3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.
(初三)
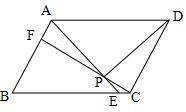
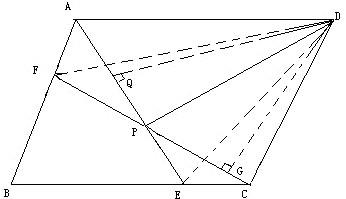
4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且
AE=CF.求证:∠DPA=∠DPC.(初二)
经典难题(五)
1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:
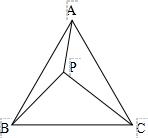
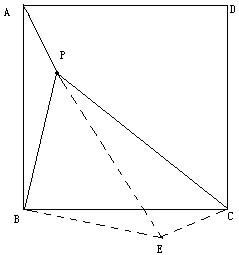
2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.
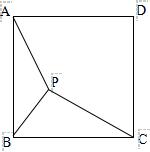
3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.
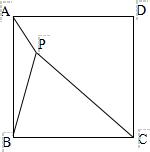
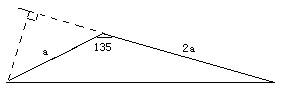
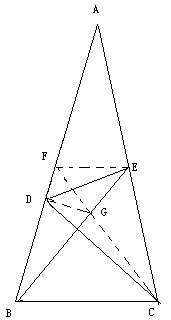
4、如图,△ABC中,∠ABC=∠ACB=80度,D、E分别是AB、AC上的点,∠DCA=30度,∠EBA=20度,求∠BED的度数.
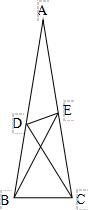
答案
经典难题(一)
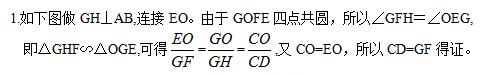


4.如下图连接AC并取其中点Q,连接QN和QM,所以可得∠QMF=∠F,∠QNM=∠DEN和∠QMN=∠QNM,从而得出∠DEN=∠F。
经典难题(二)
1.(1)延长AD到F连BF,做OG⊥AF,
又∠F=∠ACB=∠BHD,
可得BH=BF,从而可得HD=DF,
又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM
(2)连接OB,OC,既得∠BOC=1200,
从而可得∠BOM=600,
所以可得OB=2OM=AH=AO,
得证。


经典难题(三)



经典难题(四)

2.作过P点平行于AD的直线,并选一点E,使AE∥DC,BE∥PC.
可以得出∠ABP=∠ADP=∠AEP,可得:
AEBP共圆(一边所对两角相等)。
可得∠BAP=∠BEP=∠BCP,得证。


经典难题(五)

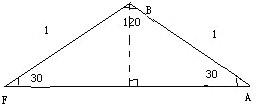

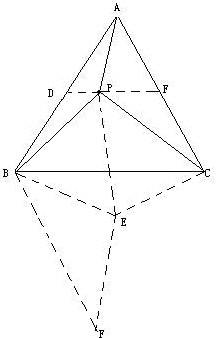
2.顺时针旋转△BPC 60度,可得△PBE为等边三角形。
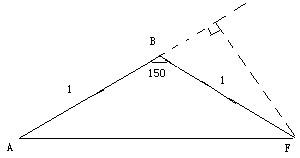
既得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,
即如下图:可得最小PA+PB+PC=AF。
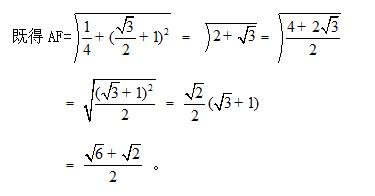
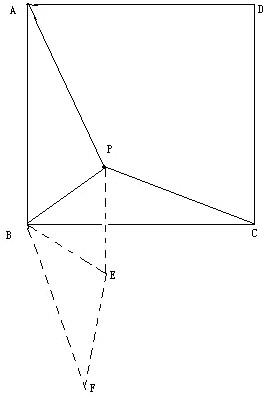
3.顺时针旋转△ABP 90度,可得如下图:
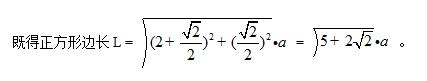

————————————

沒有留言:
張貼留言