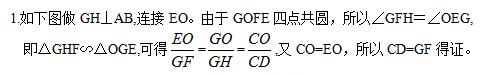关注微信:DuoDaaMath每天获得更多数学趣文
此文原载于http://centerofmathematics.blogspot.com/2015/12/famous-women-in-mathematics-and-science.html
译者,小米,哆嗒数学网翻译组成员,就读于纽约大学柯朗研究所。
时至今日,从事数学等理工学科职业的女性在数量上与男性仍相差甚远,但不可否认的是女性也能和男性在这些领域与男性一样成功:性别并能不决定一个人的智力、学习能力与潜力。我们希望下面这些优秀女性的故事能给读者以启发。
1. 希帕提娅(370,埃及,亚历山大城 —— 415,埃及,亚历山大城)

希帕提娅是希腊数学家、天文学家以及哲学家。她也通常被认为是史上第一位女数学家。希帕提娅的父亲席昂是一位数学教授;作为她的导师,他教给了希帕提娅许多科学与哲学方面的知识。约在400年时,希帕提娅成为了亚历山大城中柏拉图学派的领导者,讲授数学、科学以及新柏拉图学派的哲学。
遗憾的是,希帕提娅的许多著作在今天已经遗失,所以人们并不知道她对数学的确切贡献。人们只知道她的少数工作,例如对丢番图《算术》的评注。希帕提娅最后遭暴徒迫害杀死。我们应当记住:希帕提娅是一位受过极好教育、知识渊博的女性,并从不畏惧表达自己的观点。2009年,由其生平改编的西班牙电影《苍穹下的女神》,讲述了她波澜的一生。
2.沙特莱侯爵夫人(1706.12.17,法国,巴黎 —— 1749.9.10,法国,巴黎)

沙特萊侯爵夫人也许因她与伏尔泰的情事而出名,但许多人并不知道她在学术研究中的天分。沙特萊侯爵夫人成长在法国启蒙运动时期中的一个贵族家庭。当时的社会对像她一样的女子的期望是年经时早早结婚而不是学习知识。但沙特萊侯爵夫人说服她的父亲她需要在学术上深造,并因此获得了在当时非常良好的教育。加之她对学习的热情,沙特萊侯爵夫人在科学与数学上颇有造诣,并把它们作为终身的事业。
沙特萊侯爵夫人最著名的工作是艾萨克?牛顿的《自然哲学的数学原理》的法文翻译以及她在动能方而的研究。
她还著有《物理学教程》,讲述科学与哲学方面的最新思想;这本书原本是为她13岁儿子所写的教材。她还对哲学、神学、伦理学有所涉猎,例如她对《圣经》的分析,她对人类幸福的探讨以及她争取女性受教育权的文章。总的来说,沙特萊侯爵夫人是一位既能取得社会与家庭生活的平衡,又能持续不断地投入到科学研究与写作中的优秀女性。
3.玛丽亚?加埃塔纳?阿涅西(1718.3.16,意大利,米兰——1799.1.9,意大利,米兰)

阿涅西出生于一个富有的知识分子家庭并在意大利长大。当时的社会有学识的女子都被男子们仰慕,并被允许参加科学与艺术活动。阿涅西小时候掌握多门语言,被称为神童;青少年时已经掌握了数学。在父亲定期组织的学术交流聚会上,年轻的阿涅西也时常会跟博学的权贵客人们辩论。
尽管阿涅西对数学做出了许多贡献并展现出巨大潜力,在父亲死后她开始投身于慈善事业。阿涅西的《分析讲义》一书包含了从代数到微积分的讨论;这本为她弟弟所写的书也被认为是第一本由女性所写的数学教科书。在此书中,还出现了由一种水手结而来、被误译为“阿涅西的女巫”的曲线(方程式为 x?2;y = a?2;(a-y) ),她的名字也因此被熟知。由于她的杰出工作,阿涅西被任命为博洛尼亚大学的数学与自然哲学系主任,但因为慈善事业的缘故她从未赴任。
4. 索菲?热尔曼(1776.4.1,法国,巴黎——1831.6.27,法国,巴黎)

热尔曼出生在美国革命期间,她的童年也是在一个动荡的年代中度过:由于常常只能待在家中,她大量的时候都泡在父亲的图书馆中。正是在那里她读到了阿基米德在一个罗马士兵踩坏了他在地上画的图形后被其杀死的故事。热尔曼从此认为几何学是一个值得研究的学科,并决心学习数学;她随后在父亲的图书馆中读了大量的书籍。她的父母并不赞同她对数学的兴趣,并想方设法阻挠她,例如停掉她的暖气与照明;但热尔曼想尽一切办法反抗并坚持学习,这种情况持续到了她18岁那年,也是巴黎综合理工学院成立的时候。当时,女性并不被允许进入巴黎综合理工学院听课,但热尔曼想办法弄到了上课的讲义用以自学。最终,热尔曼向拉格朗日提交了一篇论文,用一个假名掩盖了她真实的身份。拉格朗日对她提交的论文印象深刻,并提出与写作的学生见面。他惊讶地发现作者竟然是一名女性。拉格朗日十分赞赏热尔曼的能力并成为了她的导师。拥有了一位男性导师为热尔曼打开了一扇继续学习和研究数学的大门。
热尔曼凭借她在振动弹性曲面上的工作赢得了法国科学院的奖项。这也让她跻身当时杰出数学家的圈子。热尔曼也在数论方向有所成就;她把费马大定理归结成两种情形,这在如今被称作索菲?热尔曼定理。在数论中以她的名字命名的结果还有索菲?热尔曼素数以及索菲?热尔曼等式。
5. 阿达?洛夫莱斯(1815.12.10,英国,伦敦——1852.11.27,英国,马里波恩)

洛夫莱斯的父亲-英国诗人拜伦,在她还是孩子的时候就离开她们的母女二人。因此,从小洛夫莱斯的母亲就对她在科学、数学以及逻辑学方面进行培养,希望她不会变成像父亲一样。洛夫莱斯在这些学科上表现突出,并在数字和语言上颇有天分。年仅13岁的她就设计了一架飞行器。17岁时,洛夫莱斯认识了发明家与数学家查尔斯?巴贝奇,后者成为了她的导师以及终身的朋友。正是因为这段经历,洛夫莱斯才能在科学和数学领域中做出现为人所知的众多贡献。
洛夫莱斯是第一位女计算机程序员(实际上是第一位程序员)。她做出的贡献既体现在数学也体现在计算机理论上。她最著名的工作是翻译了查尔斯?巴贝奇关于计算机分析机的论文:这个一个由查尔斯?巴贝奇发明的、可以进行数学计算的机器。洛夫莱斯提出了创新性理论并进行了复杂的理论分析。今天,埃达?洛夫莱斯日正是为了纪念她对数学与计算机的贡献以及她作为一名在科技领域的女性先驱而设立。
6.弗罗伦斯?南丁格尔(1820.5.12,意大利,佛罗伦萨——1910.8.13,英国,伦敦)
南丁格尔出生在一个上流社会的家庭,她的父母以城市的名字为他们的女儿命名。南丁格尔本可选择早早结婚并过上舒适的生活,但她却不顾家庭的反对,决心成为一名为人服务的护士。在克里米亚战争期间,她作为一名护士在俄国工作,并致力于改善医疗卫生环境,被士兵们称为“上帝派来的天使”。可惜的是,南丁格尔不久染上了克里米亚热,而在38岁时她已经难以下床。即便如此,在病床上南丁格尔仍然致力于医疗改革。直至去世,她都是公共卫生健康方面的权威。
南丁格尔因她的护士经历而为人知晓,很多人却不知道她同时也是统计学分析的先驱。在医院的时候,南丁格尔系统地收集并记录数据。她通过数据分析来改善医院的条件,并倡导卫生改革。南丁格尔还采用了许多可视化统计数据的方法,如饼图在当时就是一种相当新颖的呈现数据的方式。南丁格尔还发展出极座标图饼图,用于说明在她管理的野战医院内,病人死亡率在不同季节的变化。由于她在统计学方面做出的贡献,南丁格尔被选为英国皇家统计学会的第一个女成员,她后来也成为美国统计协会的名誉会员。
7.索菲娅?瓦西里耶夫娜?柯瓦列夫斯卡娅(1850.1.15,俄国,莫斯科——1891.2.10,瑞典,斯德哥尔摩)

柯瓦列夫斯卡娅初次对数学感兴趣是源于小时候她叔叔有一次与她的谈话。当她14岁时,柯瓦列夫斯卡娅已经自学了三角函数并开始接触更加复杂的数学概念。当柯瓦列夫斯卡娅念完中学后她希望能继续进入大学深造,但莫斯科附近的多数大学不接受女子入学。为了继续学业,柯瓦列夫斯卡娅通过婚姻离开了俄国,来到了柏林的哥廷根大学学习。当时女性不被允许进入课堂,所以柯瓦列夫斯卡娅只能接受数学家卡尔?魏尔斯特拉斯的私人辅导。在学业结束的时候,柯瓦列夫斯卡娅向大学提交了3篇论文,一篇关于偏微分方程,一篇关于木星环状结构,还有一篇是关于椭圆积分。她的论文为她赢得了一个博士学位,而柯瓦列夫斯卡娅本人却没有在大学里上过一门课。柯瓦列夫斯卡娅随后成了斯德哥尔摩大学的一名数学讲师,在此期间发表了不少数学结果以及获得了许多荣誉。虽然在41岁她因肺炎去世,但柯瓦列夫斯卡娅在她其短暂的一生中对数学做出了许多重要贡献。
柯瓦列夫斯卡娅在关于偏微分方程的论文中提出了柯西-柯瓦列夫斯卡娅定理,给出一类偏微分方程解的存在条件。她的另一著名工作是关于刚体转动的论文,这为她赢得了法国科学院鲍廷奖。柯瓦列夫斯卡娅也是女权主义及其它一些政治主张的倡导者,同时也是一名小说家、剧作家。
8.埃米?诺特(1882.3.23,德国,巴伐利亚,埃朗根——1935.4.14,美国,宾夕法尼亚,布林莫尔)

作为一名中产阶级女孩,诺特早年学习艺术,尤其是语言方面的课程。她曾经的理想是成为一名语言教师,并在毕业后拿到了教师资格证。但是,诺特放弃了教师生涯,转而学习数学并攻读博士学位。最终诺特从埃朗根大学获得了博士学位;她父亲正是这所大学的数学教授。1908年至1915年间,诺特在埃朗根数学研究所工作,在此期间她没有任何头衔和收入。在诺特的一生中这屡见不鲜:她的工作常常因为性别、政治或宗教原因而没有任何收入和认可。这一切直至诺特认识了大卫?希尔伯特和菲利克斯?克莱因才有所改变;即使大学里有许多人反对,他们仍坚持认为诺特可以成为哥廷根大学的一名讲师。最后,诺特成为了哥廷根大学的一名讲师,这是她第一份有工资的教职。不幸的是,希特勒和纳粹上台后,所有的犹太人被赶出大学,诺特也失去了她的工作。诺特随后移居美国,在布林莫尔大学教书直至去世。
在她的一生中,诺特对数学及科学做出了几项重要贡献。她最广为人知的工作是她几乎单枪匹马地发展了交换代数的理论,并强化了“理想”这个概念的应用;诺特也是第一个证明了三条环同态定理的数学家;她还证明了关于有有限理想升链的环的一系列定理,而正是为了纪念她,这样的环被命名为“诺特环”。诺特一生中发表了40余篇论文。诺特总能用自己对数学的热情去克服生活中的种种逆境。
9.玛丽?卡特莱特爵士(1900.12.17,英国,北安普敦郡——1998.4.3,英国,剑桥)

年轻的卡特莱特原本对历史学感兴趣,后来因为她觉得数学不需要记忆大量的史实因此更容易,转而学习数学。
1919年,卡特菜特进入牛津大学圣休学院学习数学,是其专业当时的五名女学生之一。两年后,卡特莱特在她的数学中级水平测试中只得到二等,这极大地打击了她;她甚至考虑过重新修习历史。但卡特莱特最终决定坚持下来,并于1923年以一等生的成绩从剑桥毕业。随后她教了四年数学,直到1928年重新回到剑桥大学格顿学院,在那里她被授予耶罗研究基金奖并发表了一系列工作。卡特莱特一生都奉献给了数学研究和数学教育,她也担任过一些管理职务。1969年卡特莱特被英国女王授予女爵士头衔。
卡特莱特一生发表了超过100篇论文,涵盖了经典分析、微分方程、拓扑等许多方向。她同时也是英国皇家学会的第一名女性成员,伦敦数学学会的第一任女主席,以及第一位同时获得皇家学会西尔维斯特奖章与伦敦数学学会德摩根奖章的女性。她的获奖为女性获得这些荣誉开创了先河。
10.茱莉亚?罗宾逊(1919.12.8,美国,圣路易斯——1985.6.30,美国,奥克兰)

罗宾逊从小在圣地亚哥长大,并就读于圣地亚哥州立大学。她的姐姐瑞德也因为写过几本关于数学和数学家的书而出名。罗宾逊最后转学至加州大学伯克利分校,并于1948年在那里获得了博士学位。毕业后罗宾逊的投入了研究工作,其中最著名的是她关于希尔伯特第十问题和博弈论的研究。1975年,罗宾逊成为伯克利的兼职教授。同年,罗宾逊成为了美国国家科学院的首名女数学家,但这只是她众多荣誉中的冰山一角。1982年她被选为美国科学学院第一位女主席,并于同一时期凭借对数学界的贡献获得了麦克阿瑟奖。
不幸的是,罗宾逊从孩童时期就被疾病缠身,最后这发展为慢性风湿热。她也因此而患上了白血病,并在65岁被夺走了生命。尽管如此,罗宾逊一生克服了种种困难并始终保持着对数学的热爱。
11.凯瑟琳?莫拉维兹(1923.5.5,加拿大,多伦多—— 至今)

莫拉维兹的父亲是一位数学家,他从小就鼓励凯瑟琳培养自己在数学和科学方面的兴趣。莫拉维兹家的家庭密友,数学家西西利亚?克里格,也鼓励凯瑟琳学习数学。1945年莫拉维兹获得了多伦多大学的学士学位,1946年她获得了麻省理工学院的硕士学位。她随后在纽约大学找到了工作,并于1951年在那里获得了博士学位。不久后莫拉维兹成为了柯朗数学研究所的一名教授。她后来成为了柯朗研究所的所长,也是美国首位担任数学研究所所长的女性。
莫拉维兹早期的工作是研究超音速波与激波。随后她开始研究音波以及电波碰撞物体后的散射问题。莫拉维兹在的研究中得到了一系列关于非线性波方程弱解的重要结果。由于她对数学做出的杰出贡献,莫拉维兹在1998年成为首位获得美国国家科学数学奖章的女性,这是美国在科学领域的最高奖。莫拉维兹还获得过杰弗里-威廉姆斯奖,伯克霍夫奖及洛瑞?斯梯尔数学终身成就奖。
12. 玛丽安?米尔扎哈尼(1977.5,伊朗,德黑兰——至今)

米尔扎哈尼在少年时期就表现出相当的天分,曾就读于伊朗国家天才儿童发展组织的建立的一所中学中。初中时期米尔扎哈尼的理想是成为一名作家,但高中时她决定投身于数学。米尔扎哈尼在数学上取得了优异的成绩。在1994年和1995年国际数学奥林匹克竞赛上。米尔哈扎尼获得金牌,并在1995年的比赛中获得满分。她随后就读于谢里夫理工大学,毕业后决定前往美国深造。米尔扎哈尼在哈佛大学获得了博士学位,同时也是克雷数学研究所的一名研究员。2008年至今,米尔扎哈尼在斯坦福大学担任教职。
米尔扎哈尼于2014年获得菲尔兹奖,是有史以来首位获奖女性。这是为了表彰她在”黎曼流形及其上模空间的动力学与几何学上做出的贡献”(国际数学联盟)。米尔扎哈尼还获得过许多其它荣誉,包括鲁思该萨特数学奖、布卢门撒尔奖等等。米尔扎哈尼在数学方面的工作以及她获得的荣誉,表示人们正逐渐接受女性在这个领域中取得成功。