「數學王子」高斯的生平與數學貢獻,難以想像的超級天才
高斯(全名:卡爾·弗里德里希·高斯)是數學史上最偉大的數學家之一,大概也是所有人最早認識到的數學家。大家在學校應該都聽過,高斯在九歲時,就解開了老師出的「從 1 加到 100」的數學題。他用的方法是,把頭跟尾相加,變成 1+100、2+99、3+98,這樣一來,就可以得到 50 個 101 ,所以答案就是 50 x 101 = 5050。他一生在數學、物理學、天文學、大地測量學的貢獻良多,又有「數學王子」的稱號。

高斯的生平
高斯生於 1777 年 4 月 30 日,於是 Google 將今天的 Google Doodle 作為紀念。據傳,高斯從三歲起就能糾正商人父親與會計記帳時的錯誤、九歲時解開老師出的等差級數問題、12 歲時,已經開始懷疑幾何原本中的基礎證明。當他16歲時,預測在歐氏幾何之外必然會產生一門完全不同的幾何學,也就是非歐幾里德幾何學。他導出了二項式定理的一般形式,將其成功的運用在無窮級數,並發展了數學分析的理論。
簡單來說,高斯就是過著一個天才般的人生,不斷的將當時數學的發展推進。
高斯的重大貢獻
質數定理
「質數」代表不能被其除了 1 和自己本身以外的數整除的數字,像是 3、5、17、23 都是。世界上有無數多個質數,而高斯提出了質數的分布會隨著數字不斷變大,而變得越來越「稀疏」。一直到 1896 年才由法國數學家雅克·阿達馬提出證明,證實此一現象。
正 17 邊形的尺規作圖
不曉得現在高中還有沒有教過「尺規作圖」。這是透過尺還有圓規來畫出各種圖形的技術,但不能夠使用齒的刻度,圓規也不可以有丈量角度或長度的功能,所以要畫一個單純的垂直線,就必須要用這類麻煩的方式:
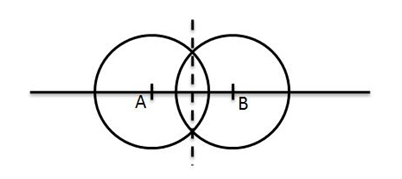
所以,光是要畫個正五邊形就不容易了,高斯卻能夠在 19 歲時,提出「正 17 邊形」的尺規作圖法:
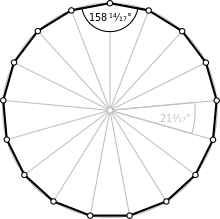
畫法如下:

複數的應用
繼續幫大家複習數學,所謂「複數」,就是指帶有「虛數 i」(負一的平方根)的方程式解。在高中時,大家應該都記得「N 次方程式有 N 個解」這件事,這就是建立在複數的基礎之上的。而高斯總結了複數的應用,並嚴格證明了每一個 n 階的代數方程必有 n 個實數或者復數解的概念。
成年後的高斯,除了在數學領域上繼續探索外,也進行了許多地理、天文的探索工作。並發明了日光反射儀、強磁針等儀器,在許多領域上都有卓越的貢獻,像是現在磁場的位置、電報的發明,都有高斯的影子在其中。
Google Doodle 上的圖示與發明對照
在紀念高斯冥誕的這一天,Google Doodle 透過簡單的圖示列舉了高斯的一些貢獻。
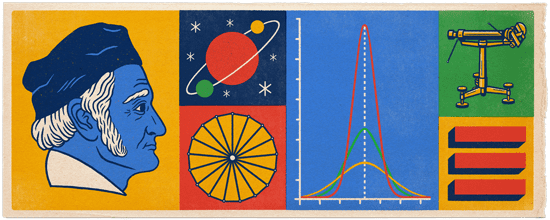
- 計算行星軌跡:高斯在最小二乘法基础上創立的測量平差理論的幫助下,計算天體運行的軌跡,並依此方式測算出了小行星「谷神星」的運行軌跡。
- 正 17 邊形的尺規作圖法:在前面提過,高斯在 19 歲時就解決了這個極難的數學問題。
- 高斯函數:
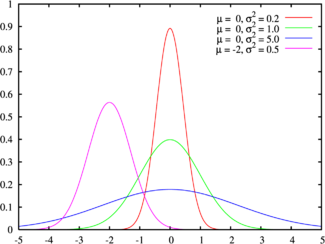
- 電報機:高斯與韋伯發明的電報機
- 同餘符號:最後的三條線代表著「≡」,也就是數學上的同餘符號;最先引用同餘概念與此符號者也為高斯。(感謝讀者佳修來信)
高斯的歷史地位
高斯的肖像在 1989~2001 年底,被放在德國 10 馬克的鈔票中,德國也發行了三種表彰高斯的郵票。在 2007 年時,他的半身像被引進瓦爾哈拉神殿中。其中,月球上的坑洞、小行星 1001 也被稱為「高斯星」。

用於磁場的 CGS 單位也被稱作「高斯」。

沒有留言:
張貼留言