【我的數學夢】尋找狐狸的足跡
2011
五月
3
■ 「有些事現在不做,以後也不會做了!」這是一個法律系學生熱血前進數學的故事,在他眼中,法律與數學並沒有那麼的不同。
撰文 ∣ 戴佳原
國一時我一直不明白為什麼x+2=3會得到x=1,而不是x=x這個不言自明的答案。更不明白為什麼當我這樣回答,考試總是零分。我的疑惑,那 時沒有人能解答。直到有一次家政老師看我在算數學,她和許多人一樣,也不懂為什麼我不會那麼簡單的問題,但不一樣的是,她很大方地嘲笑我,而我哭了,但命 運很奇妙,我從此就會了。
後來,我讀了些數學哲學,知道人類從數覺(如一隻羊)到數(如抽象的1),從結繩到符號,必須經歷幾萬年的演化。才知道當時在我的生命中也經歷了演化,雖然只有幾個月,但已讓我如此強烈地意識到數學的存在。
高中,不知是否因為經歷某種佛洛依德式的不滿足,我變得擅長操弄符號,加上一點耐心,成為了解題能手。某次高二數學課,老師透過矩陣求解一般線性方程組,我看著黑板上的x,y和z,突然想起國中懵懂的自己,再想起現在卻能處理那麼多未知數,不禁激動難以自已。
人生許多選擇,探尋到最後,驀然回首,都是這些回憶碎片。
我曾申請台大數學系,但感謝神,我落榜了。原本父母希望我去念森林系,因為他們認為我是個太「條直」的孩子,比較適合去跟樹在一起。不過最後我 透過指考進入了台大法律系。不知為何,我對數學念念不忘,於是大二時申請了雙主修數學系,因此我常自嘲為「法數系」學生。有些法律系同學認為法律跟數學很 不「搭」,甚至認為既然都讀法律,就不再需要數學或科學。然而,我認為人類事務極其複雜多元,法學在知識面上不可避免地要與哲學、政治學、經濟學、社會 學,甚至自然科學「先衝突後整合」,才能妥善處理各種紛爭。這種體認不但是我選擇法律系的初衷,也促使我思考如何在近代學科專業分化的趨勢中,提醒自己保 持寬闊開放的學術心胸。為此,當時年輕狂妄的我,琅琅上口「法律數學本一家」,理所當然引起不少質疑。
為了證明自己是對的,我研讀一些「學術史」方面的書籍,了解數學(或數學哲學)在啟蒙時代後引起方法論的風潮,例如Bentham相信功利主 義,想建立「快樂的微積分」來分析如何極大化社會福利;美國憲法具有數學公理化演繹邏輯的風格;在自然法與純粹法學的概念中也可看到數學的影子。直到現 在,「非線性」、「蝴蝶吸子」、「混沌」和「拓樸」等數學術語也納入刑法學、哲學和歷史學關於因果關係的討論。當然,以上例子無法充分釐清「法律數學本一 家」中「本一家」一語所具備的歧義性,而學科術語跨界混用也值得省思,但一路走來,我始終相信,積極開放心胸會讓學術生命將更為豐富。
並不孤獨
讀過歷史上許多數學家的學思經歷之後,我發現兼具法律與數學訓練的人其實不少!例如笛卡兒(René Descartes)是法學博士,是律師;費馬(Pierre de Fermat)也是律師;萊布尼茲(Gottfried Leibniz)大學主修法學;惠更斯(Christiaan Huygens)大學主修法律與數學;魏爾斯特拉斯(Karl Weierstrass)承父命在大學主修法律與財政,但為了數學,據說他寧可酗酒,向他父親抗議。他們出入於法律與數學之間,讓我知道自己並不孤獨。
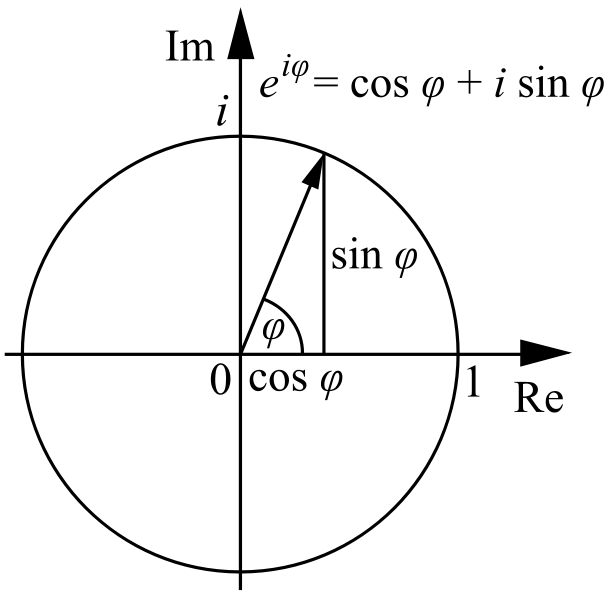
但到底是什麼吸引我的這些「法數系」學長們如此熱愛數學,甚至奉獻一生?從真善美的角度,我認為,數學「公理化演繹邏輯」的方法論能產生其他學 科無法擁有的「確定性」。為此,數學思考近似接觸真理,數學證明則等同發現真理。另外,數學總散發著一種簡潔純粹的美感,例如我最喜歡的Euler公式: eiπ + 1 = 0,一個簡單等式結合了加法、乘法和指數律等常見運算,以及Euler數e、虛數i、圓周率 、乘法單位元素1和加法單位元素0等宇宙中最重要的幾個常數。
然而,數學很美,數學也很難,抽象的符號系統是數學「冷峻」的一面,也是不少人「害怕」數學的源由。不過,只要回想幾世紀前的數學家們以藝術看 待數學,並認為數學能發現預測宇宙規律,榮耀創造萬物的上帝,或許「冷峻」就只是真理之門前的大理石雕像,要人們心懷敬虔而謙遜。至於善,數學在所不問, 所以數學「可能無益,但絕對無害」。拿著紙筆,讓心靈依循著直覺前進,透過邏輯一步步整理足跡,直至真理之門,多麼自由與和平!
雙主修數學系後,我得以比較中學數學與高等數學的異同。解題是數學的核心,中學數學著重計算,題意、條件與答案明確,只要看清一兩個「眉角」加 上些許耐心即可駕輕就熟。高等數學則著重證明,透過各種數學結構的細膩分析來「一網打盡」相關問題。例如為了處理極值問題,中學數學發展出算幾不等式及柯 西不等式,但只能處理一小類問題。微分學的極值檢定法,則幾乎能處理各種極值問題。不過事實上,不論在中學或大學,類推比較、以簡御繁及分類化約一直是我 們處理數學問題的基本思維,只是高等數學需要更細膩的觀察、更神妙的巧思以及更繁複的運算。以類推比較為例,Fourier級數中的Parseval等式 是中學畢式定理的類推,然而,類推的過程絕對是數學家們充滿挫折的奮鬥史。
為什麼高等數學需要更多奮鬥?原因在於「面對無窮」並「馴服無窮」是高等數學永恆的任務。以積分學為例,為了計算曲形面績(如橢圓面積),由於 線形。面積(如矩形面積)計算容易,透過以簡御繁的思維,我們會用數個線形面積的總和去「逼近」曲形面積,再論證當線形越來越多,則所有線形面積的總和會 「等於」曲形面積,而非逼近。以上論證的關鍵處是「無窮過程」,亦即「從有窮到無窮的飛躍」如何成立!數學史告訴我們,從古希臘時代就有「無窮的恐懼」, 而近現代,無窮級數的收斂性是分析學的基本問題,無窮的分類則豐富了拓樸學,許多由無窮產生的悖論一直是惱人而重要的數學問題,直到兩千多年後,本世紀六 〇年代的非標準分析學才真正馴服無窮。
我的數學思想史
猶記得那天早晨天氣晴朗,在新數101教室,林紹雄老師證明高等微積分的Heine-Borel定理。當證明寫完後,我感動到不可自禁地驚呼: 「人類怎麼想得出來!」而且,老師說數學界花了三十年才發現並證明這個定理。那時,我告訴自己,一定要發掘這三十年來數學家們探索的過程,因為人類挑戰了 看似不可能的事物。為此,我開始研讀數學史,先反思微積分學的發展,發現教科書的內容次序:「極限→連續→微分→積分」,竟然與數學史「積分→微分→連續 →極限」的發展背道而行!我意識到原來文章書籍的「邏輯理路」(the way of logic)與數學思考的「探索理路」(the way of discovery)可以如此不同。當然,邏輯理路直接明快,像食譜一樣,學習者一步步照做即可,但缺點是常常覺得「天外飛來一筆」。至於探索理路,葛兆 光先生的《中國思想史》給我不少指引,他認為在思想史研究中,展現知識積累與發展的「加法」固然重要,然而,找回思想被刪減隱沒的「減法」更有啟發。阿貝 爾(Niels Henrik Abel)曾形容高斯(Carl Friedrich Gauss)像一隻狡猾的狐狸,在沙漠上一面行走,一面用尾巴抹掉足跡,探索理路就是「重現」被抹去的足跡,這就是我的數學夢,我的「數學思想史」!
於是,我決定報考數學研究所,不少人關心我,提醒法律系出路較為寬廣。不過,或許受到影片《練習曲》中那句話的鼓舞:「有些事現在不做,以後也不會做了!」我相信,走上數學之路的決斷,我不會後悔。
就讀數學研究所那兩年,我不再擁有法律與數學的「雙重身份」,我必須完全獻身在「典範」中。我的碩士論文以生態學上的反應擴散方程為主題,她是 一份不錯的文獻回顧,因為我盡可能以探索理路的方式呈現,雖然我曾努力,想要發現屬於自己的命題與證明。在碩士階段,我深刻體會到「研讀數學」跟「研究數 學」是兩回事,以及研究數學思想史之前,必須先精通數學。
夢想之路上有時花朵繽紛,有時荊棘坎坷,但我的神,我的數學夢引領我,即使迷霧重重,我仍能大步前行。如今我在服兵役,退伍後即將去柏林自由大學參加數學博士班面試。未來充滿可能性,而我還年輕!
作者簡介
戴佳原,台灣大學法律系法學組92級,台灣大學數學研究所畢。
他的自述:「去年新訓,常常得在嘉義的美麗夕照下,全副武裝持槍肅站重覆背頌國軍準則,而那時,我的心中是滿滿地渴望留學德國、鐵馬環球與當好爸爸。」
責任編輯:MissZoe本文為CASE專題「我的數學夢」連載第三篇。


沒有留言:
張貼留言