我們想讓你知道的是
這個超級大質數是由美國田納西州一位FedEx員工名叫佩斯發現的,至於要怎麼找到這麼大的質數,當然是少不了電腦,據說他用的電腦cpu 是 Intel quad-core i5-6600,跟我們一般家用電腦差不多而已。
文:陳宏賓(UniMath主編,逢甲大學應用數學系助理教授)
所謂質數就是除了1和本身之外無法被其它正整數整除的數,例如:2、3、5、7、11......代數很重要的一件事說,任何大於1的整數都可以唯一表示成一些質數的乘積。整數裡質數的地位感覺就好像是色彩之於原色。
你對五十個人說出「紅色」這個詞,可以想見他們腦中會浮現五十種紅色,而且幾乎能確定的是沒有一種紅色是一樣的。關於「數學的美」,我想也差不多。我最愛的數學家保羅艾狄胥是這樣子說的:
「就好像你問貝多芬的第九號交響曲美妙在哪,如果你聽不出來為什麼它美,那麼也沒有人可以告訴你。我知道數字很美,如果它們不美的話,沒有事物稱得上美了。」
完美數
在很久很久以前,有一類數被古希臘數學家認為很美好,它們可以寫成自己所有正因數(除了自己)的和,這樣的數就稱為「完美數(perfect numbers)」。例如6的正因數有1、2、3、6,剛好1+2+3=6;28的正因數有1、2、4、7、14、28,剛好1+2+4+7+14=28,所以6和28都是完美數,每年的6月28日也因此被稱為「完美日(perfect day)」。

最小的完美數就是6,是我自從大學系籃開始至今愛用的球衣號碼,期望每一次上場都能有完美表現,不過,you know,還是經常失誤,有時連罰球也投不進。多練習還是比迷信有用啊。
今年的1月3日,史上最大完美數被發現了,不過,我的電腦螢幕空間太小,所以我無法寫下來(我打賭費馬三百多年前的梗就算再過三百年還是會有人用XD)不過,這裡我說的空間太小寫不下來是認真的,等一下你就知道要一一寫下每個位置的數值是多麼巨大的工程,連用嘴巴唸一遍你都會嫌麻煩。如果你不介意我偷懶,倒是可以寫成這種形式
277232916(277232917-1)
外表看起來有點醜陋的它,內心是完美的。真的,我保證。你可能依然不相信。
不過,也由不得你不信,數學家總是這個樣子。很久很久以前,數學界的先賢歐幾里得心裡的完美數就清清楚楚了。
只要2n-1是質數,那麼2n-1(2n-1)就是完美數。
從現代數學的眼光來看,這倒是只需要一點點因倍數和等比級數的數學觀念就夠了。
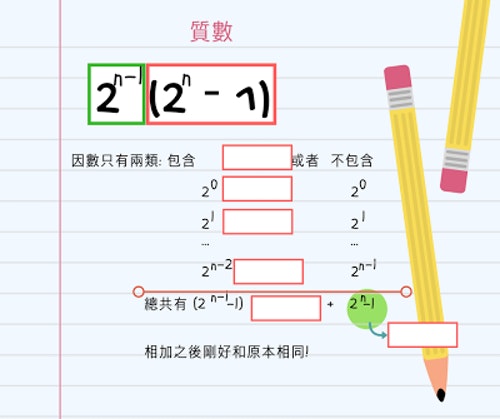
歐幾里得在大約2,300年前就知道這種事也太令人佩服了啊!一千多年以後,另一位超人級的數學家歐拉提出更進一步的結論:
所有偶數的完美數都必然長這個形式2n-1(2n-1)。
截至目前為止,這世界上沒有人知道,是不是有無窮多個完美數(基於讓這個世界更完美一點的想法,我希望完美數是無窮多的);同時,也還沒有任何一個人曾經見過奇數的完美數,如果你遇見它,請帶我去那個地方。
超級質數任務
前幾天,Great Internet Mersenne Prime Search(GIMPS)這個組織公布目前最大的質數277232917-1,這是一個高達23,249,425位數。這個超級數字到底有多大呢?打個比方,假設有一個全世界第一快嘴每秒鐘能夠讀10個數字,那麼即使他不吃不喝不笑不走路,把這個數從頭到尾讀一遍也得花上將近一個月的時間。
這個超級大質數是由美國田納西州一位FedEx員工名叫佩斯發現的,至於要怎麼找到這麼大的質數,當然是少不了電腦,據說他用的電腦cpu 是 Intel quad-core i5-6600,跟我們一般家用電腦差不多而已耶,不過用此等級的電腦檢驗這個超級質數可是要花上好幾天才行。
話說回來,具備這種型式2n-1的質數有個特別的名稱,叫做Mersenne Primes梅森質數。顧名思義,這是為了紀念17世紀專門研究這種數的一位法國僧侶Marin Mersenne。這種型式的質數,其實並不常見,截至目前為止也才50個被發現,其中的17個是由GIMPS或藉由GIMPS提供的程式找到。GIMPS也發下豪語,提出高達150,000美金(約台幣四百多萬)的獎勵,看誰能先找到超過一億位數的超級質數。
不曉得挖比特幣跟尋找一億位數超級質數哪個投資報酬率比較好呢?你準備好了沒。



 。
。