用數學幾何蓋出沒有柱子的建築!巴爾蒙德的倫敦蛇形藝廊 2002
英國倫敦海德公園旁,曾有一棟相當著名的實驗性建築蛇形藝廊 2002(Serpentine Gallery Pavilion 2002),蛇形藝廊從 2000 年開始每年都會在夏季舉辦為期三個月的建築展覽,結束後會拆除隔年再換下一個實驗性建築,世界上許多建築大師都曾參與其中[1],算是建築界非常有名的年度盛事。
蛇形藝廊 2002 是由建築師伊東豊雄(Toyo Ito)、結構設計師塞西爾.巴爾蒙德(Cecil Balmond)與 Arup 團隊共同完成,是一棟長寬高為 18 m × 18 m × 4.5 m 的建築物。意外的是建築內沒有看到明顯的柱體,反而是由許多直線交織出不規則的圖形,來構成天花板與牆面,使得建築物散發一種特殊的美感。具體上無法形容和說明這個建築帶給我的感覺,但從數學人的觀點來看,這構造和幾何息息相關。
建築的最基本元素是正方形?!
乍看之下,建築物中的線條十分複雜看不出有什麼規律,但實際上裡頭運用了非常簡單的數學原理與演算法規則。結構設計師巴爾蒙德在建築結構設計中,運用許多典型之外(informal)的設計方式[3],改變一點大家習以為常的規則,創造出許多有趣的建築。
在蛇形藝廊 2002 的建築設計中,巴爾蒙德以正方形為元素(element)作為設計結構的思考起點。他將一個正方形的其中一邊的中點也就是 1/2,連至鄰邊邊長的 1/3,以此類推至四個邊,卻發現這四個邊無法構成一個正方形,所以再將這四個邊的邊線延伸至出去,得到了一個小正方形。再按照此 1/2 → 1/3 演算法的原則進行多次之後得到如下圖右下方交錯的線條網路[4]。
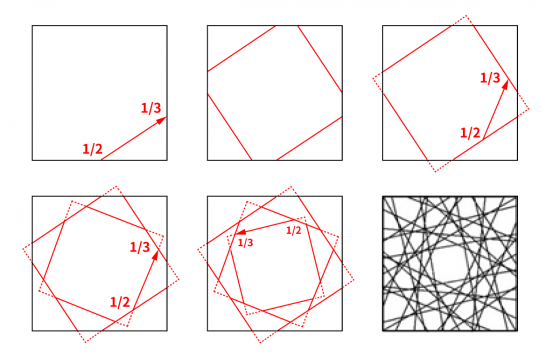
我們一般人如果想要在正方形中得到另一個正方形,大概就是 1/2 → 1/2 原正方形四個邊的中點連中點吧。1/2 → 1/3 的演算法和 1/2 → 1/2 有什麼不同呢?
首先是中心點與胚騰〔註〕的偏移(skew of pattern)打破了原有圖形的對稱性,新的正方形會超過原本正方形的邊界,在重複進行多次以後也會產生螺旋的形狀。
- 註:胚騰(pattern)可解釋成圖樣、紋理、規律、規則等。
接著選定正方形內較小的一四邊形當作屋頂設計的樣式後,去掉四個角落之後將四邊形外多出的線條垂直向下摺疊 90 度形成一個盒子,再進行結構分析選擇哪些空間是具乘重功能的結構體、哪些空間則保持簍空,使整個系統成為一個無傳統梁柱的建築結構系統。也就是說,這個造型本身就是結構體,而不是只有外觀裝飾功能。
沒有柱子的實驗建築誕生
其實最一開始的時候,伊東豊雄了解到可以在材料與型式上進行許多實驗,由於只有三個月的展期,因此不用擔心建築的功能,也無須擔心建築物會隨著時間老化的特性。他和巴爾蒙德打算採用一般的盒形幾何,透過胚騰的參與(patterned intervention)轉化成一個特殊且與眾不同的建築。
伊東在概念發想階段提出兩個問題:第一是如何將一個樓板漂浮在空中,也就是說沒有可見的鉛垂線,亦沒有傳統上樓板在柱子上的限制;第二個問題則是如何轉化一個盒子?也就是做一個沒有柱子甚至沒有窗戶與門的盒子(column-less box)[5],沒有任何一般建築會有的元素。
總而言之,伊東想要呈現的是非線性的過程。他們想出的策略是秩序的隨機(ordered random),看似隨機但背後隱含著秩序。伊東交了一個有很多大型不規則氣泡在建築體的草圖給巴爾蒙德之後,巴爾蒙德修正提出了 1/2 → 1/3 的演算法,將乾枯的算術轉化成可用在結構、建築、裝飾的代數規則。
具備將元素轉化成結構設計規則這種能力的結構設計師並不多,巴爾蒙德在這方面是佼佼者,世界上許多知名的建築師都喜歡找他合作。2016 年重新開幕的台中歌劇院也是伊東豊雄和巴爾蒙德的作品,看歌劇院流動的造型就知道他們總是喜歡挑戰一些高難度的建築。
用「元素」玩出結構新貌 巴爾蒙德的建築世界
除了前述的從元素正方形中設計出建築的基本構造之外,巴爾蒙德也擅於從大自然的元素中提取設計的靈感還寫了一本叫做《元素》(Element)的書[6],裡面有稻草堆、花朵生長的方式、甚至還有一個章節是數學裡面的元素,像是伊斯蘭圖樣、數字等概念。
巴爾蒙德早期也曾經研究過位數根(digital root),憑藉著對數字的熱愛以及其中蘊含的規律,寫了《數字 9》(Number 9 : The Search for the Sigma Code)這本書,裡頭也有提到源自古印度數學的吠陀方形(Vedic square)以及位數根的各種規律[7],下圖是吠陀方形在 Element 展覽中呈現的樣態;最新的書 Crossover 則是整理了以往的藝術、建築、橋梁的創新設計案例與概念[8]。

Cecil Balmond 的著作。圖/Amazon
雕塑家朱銘說過:「人類創造立方體,卻被立方體所框。」他認為自然生態之中並沒有立方體的型式存在,而僅存在於人類社會之中。被創造出的立方體對人的生活空間與思考都是一種框架,朱銘也在思考如何跨越這個限制。
巴爾蒙德創造出了一個立方體,顛覆了一般大眾對於立方體的認知,以及建築設計、工法上的限制。以秩序生成隨機體現於建築中,不再被立方體所框,而這一切不過就是一個正方形從 1/2 連到 1/3,將線條延伸出原本的邊界去。
讀巴爾蒙德的書除了覺得對於數學的著迷這一點與大師心靈相通之外,還發現他的書書名可以寫成一個跨界方程式:仔細觀察自然或數學中的元素(Element),乘以別人想不到的非典型方式制定新規則(Informal),便可以跨越邊界創造新事物(Crossover)!
Element × Informal = Crossover
- 此文作者本系列文章獲得臺北市政府文化局藝文補助
參考資料:
- Pavilion | Serpentine Galleries, 2016.
- Balmond Studio, 2016.
- Balmond, C. Informal, Prestel, Munich, 2007.
- Lin, C. Y. Digital Root Patterns of Three-Dimensional Space. Recreational Mathematics Magazine, 3(5), 9–31, 2016.
- Ito, T., Balmond, C. Serpentine Gallery Pavilion 2002: Toyo Ito with Arup, Workshop for Architecture and Urbanism, Japan, 2002.
- Balmond, C. Element, Prestel, Munich, 2007.
- Balmond, C. Number 9, Prestel, Munich, 1998.
- Balmond, C. Crossover, Prestel, Munich, 2013.










